Files and directories¶
config/¶
config.dat¶
config.dat contains the measurement configurations to be modelled. A
measurement configuration is defined by one or two electrodes used for current
injection and one or two electrodes used for voltage (i.e. potential
difference) measurement. By this, pole-pole, pole-dipole, and dipole-dipole,
(multiple)-gradient configurations can be realized. The format of
config.dat is explained by means of an example file:
1 2064
2 10002 40003
3 10002 50004
4 10002 60005
...
...
...
2063 300036 220016
2064 300036 230017
2065 300036 240018
Line 1: Number of measurement configurations
Line 2-End: Dipole configuration. The first number describes the current injection dipole using the formula \(A \cdot 10000 + B\). The second number describes the voltage dipole using the formula \(M \cdot 10000 + N\).
Pole-pole or pole-dipole configurations are realized by assigning a fictitious
electrode ‘’0’’ (representing infinity) to the corresponding position in
config.dat. For example, the line:
10000 20000
would define a pole-pole measurement, the line
10000 20003
a pole-dipole measurement.
exe/¶
crt.lamnull¶
In order to have the option to preselect a starting value for our pareto
problem (lambda search), we introduce the lamnull_cri and lamnull_fpi
variables which can be set by the user via the file crt.lamnull.
This can contain two variables:
<lamnull_cri> (double)
<lamnull_fpi> (double)
The last one may be left empty (defaults to zero then). They are used in the
subroutine blam0 to set the lammax value.
If a complex (CRI) or DC inversion is done, the variable lamnull_cri is used.
For FPI we can use the variable lamnull_fpi, which is a NEW option.
Introduction of a separate value for the FPI is done because of two reasons:
lam0 for the FPI changes usually dramatically if the model is changed, thus, the preselected values of lam0 for FPI may totally differ to the value for the CRI/DC.
practical reasons for synthetic study
DEFAULT Value:
If a value of zero is choosen for each one of the lamnull_*, the program chooses:
\(\sum(diag{J^TJ})/<\text{number of parameters}> \cdot 2 /(\alpha_x + \alpha_y) * 5\)
The first is obvious, because we like to scale upon the ‘’mean’’ entries of our sensitivity matrix.
The scaling is done then to take the artificial anisotropy regularization (\(\alpha_x\) and \(\alpha_y\)) into account and last but not least multiply by five just to make sure we start right at the upper most boundary for the pareto problem.
crtomo.cfg¶
Note
Configurations can be created, imported, modified, and saved using
crtomo.cfg.crtomo_config.
Also see example here: Setting modeling and inversion settings
The crtomo.cfg file controls the inversion using CRTomo. It must exist
in the directory where CRTomo is executed. Lines starting with the
character # are treated as comments and will be removed before parsing it. All
other lines are line-number dependent. That is, each setting is identified by
its line number, not a keyword, within the crtomo.cfg file. Comment lines
do not increase the line number!
The first non-comment line is a multi-function binary switch called mswitch. This switched controls functions by setting their corresponding bit either to 0 (inactive) or 1 (active).
Note
Use crtomo.cfg.crtomo_config.set_mswitch() to control the mswitch
in a Python environment
The following functionality is implemented, with the corresponding bit given at the beginning:
*** : legacy values - treated a 0
bit 1 (+1): write L1 data-weighted coverage (lsens)
bit 2 (+2): write out main diagonal of posterior model covariance matrix: \(MCM_1=( A^T C_d^-1 A + \lambda C_m^-1 )^-1\) (lcov1). Note that enabling this function also writes out \(diag(A^T W_d^T W_d A)\), the L2 data-weighted cumulative sensitivity (or coverage) into the file ata.diag.
bit 3 (+4): write out main diagonal of resolution matrix: \(RES = MCM_1 * A^T C_d^-1 A\) (lres)
bit 4 (+8): = write out main diagonal of posterior model covariance matrix 2: \(MCM_2 = RES \cdot MCM_1\) (lcov2)
lgauss = BTEST (mswitch,4) ! +16 solve all OLS using Gauss elimination
lelerr = BTEST (mswitch,5).OR.lelerr ! +32 uses error ellipses in the inversion, regardless of any previous lelerr state..
mswitch with 2^6 is empty for now…
lphi0 = BTEST (mswitch,7) ! +128 force negative phase
lsytop = BTEST (mswitch,8) ! +256 enables sy top check of no flow boundary electrodes for enhanced beta calculation (bsytop). This is useful for including topographical effects
lverb = BTEST (mswitch,10) ! +1024 Verbose output of CG iterations, data read in, bnachbar calculations…
The file is further described by an example file:
1#############################################################
2### NEW cfg file format:: ###
3#############################################################
4### Comment lines start with (at least one) # at the first
5### row of a line !
6### They are omitted during import of the cfg file
7#############################################################
8#############################################################
9## NOTE:
10## NO FURTHER EMPTY LINES, EXCEPT THE ONES ALREADY PRESENT,
11## SHOULD BE ADDED. CRTomo IDENTIFIES PARAMETERS BY THEIR
12## LINE NUMBER
13##############################################################
14##############################################################
15#############################################################
16# mwswitch (8 == lcov2)
178
18#############################################################
19# Path to the grid file, may contain blanks
20#############################################################
21../grid/elem.dat
22#############################################################
23# Path to the file containing electrode positions, may contain blanks
24#############################################################
25../grid/elec.dat
26#############################################################
27# Path to the measurement readings (Volts!), may contain blanks
28#############################################################
29../mod/volt.dat
30#############################################################
31# Directory name to store the inversion results.., may contain blanks
32#############################################################
33../inv
34############################################################
35# Logical switch for difference inversion (ldiff) and, if a prior model (m0) is used,
36# this switch also controls whether or not to regularize against the prior..
37# (internal variable lprior=T)
38# leading to (m-m0)R^TR(m-m0) constraint, if no difference data are given
39#########################################################################################
40F
41#########################################################################################
42# Path to the measurement file for difference inversion, may contain blanks.
43# If left empty, no data is assumed
44#########################################################################################
45../diff/dvolt.dat
46#########################################################################################
47# Path to the prior model (m0), which is also the model of the difference
48# inversion which is obtained by a previous CRTomo run (dm0).
49# If ldiff is false, and a valid path to a prior is given,
50# the prior is copied into the starting model!!
51#########################################################################################
52../rho/prior.modl
53#########################################################################################
54# Path to the model response of m0 in case of difference inversion (ldiff=T)
55# this should be empty if you have none
56#########################################################################################
57../diff/dvolt2.dat
58#########################################################################################
59# The next line usually contains nothing but *** ....
60# YET, if you have a prior (or starting) model and like to add noise to it.
61# You can then give a seed (integer) and a variance (float) for this.
62# These numbers are useless if no prior is given..
63#########################################################################################
64iseed variance
65#########################################################################################
66# For regular grids and the old regularization you have to define the Nx (number of
67# elements in x-direction)
68# THIS IS NOW OBSOLETE (but can be used, though..) because the triangulation
69# regularization is proofed equivalent to the old regularization for regular grids!
70#
71# To give it a new purpose, you can now control variogram models with it!
72# The integer is read in as decimal leaving two digits (XY) with a control function
73#
74# _X_ Controls the covariance function and _Y_ the variogram model
75#
76# The variogram model has 4 modes:
77# CASE (X=1) !Gaussian variogram = (1-EXP(-(3h/a)^2))
78# (Ix_v = Ix_v/3 ; Iy_v = Iy_v/3: scale length are changed to match GSlib standard)
79# CASE (X=2) ! Spherical variogram = ((1.5(h/a)-.5(h/a)^3),1)
80# CASE (X=3) ! Power model variogram = (h/a)^omev
81# in this case you can change the power model exponent, which is set to 2 as default
82# CASE DEFAULT! exponential variogram = (1-EXP(-(3h/a)))
83# (Ix_v = Ix_v/3 ; Iy_v = Iy_v/3)
84# The default case is used if left at zero or otherwise
85#
86# For the covariance function there are also 4 modes implemented:
87# CASE (Y=1) !Gaussian covariance = EXP(-(3h/a)^2)
88# (Ix_c = Ix_c/3 ; Iy_c = Iy_c/3: scale length are changed to match GSlib standard)
89# CASE (Y=2) !Spherical covariance = ((1-1.5(h/a)+.5(h/a)^3),0)
90# CASE (Y=3) !Power model covariance = EXP(-va*(h/a)^omec)
91# CASE (Y=4) !Lemma (still to proof!) covariance = EXP(-tfac*variogram(h))
92# CASE DEFAULT!Exponential covariance = EXP(-3h/a)
93# (Ix_c = Ix_c/3 ; Iy_c = Iy_c/3)
94#
95# The covariance model does only makes sense with a stochastical regularization!!!
96#
97# EXAMPLE:
98# - You like to have spherical variogram but gaussian covariance set the number
99# to 12
100# - If you like to have a spherical variogram and a exponential covariance
101# NOTE:
102# The experimental variogram can be calculated (and this is default if any value
103# is given) no matter which model function you state here..
104#########################################################################################
1050
106#########################################################################################
107# Previously, the next integer number was the number of cells in z- (or y)-direction
108# However, the same argumentation for this number holds as for Nx.
109# The new meaning for Nz is now to give a starting value for lambda:
110# -value given here sets lam_0 = value
111# This may be further exploited (in case you do not know and do not like the whole A^TA
112# diagonal maximum to be calculated (blam0), you can leave it as -1 which will take
113# lam_0 = MAX(number of data points,number of model parameters)
114#########################################################################################
115-1
116#########################################################################################
117# Now, the anisotropic regularization parameters (float) can be specified:
118# alpha_x
119#########################################################################################
1201.0000
121#########################################################################################
122# alpha_z (y)
123#########################################################################################
1241.0000
125#########################################################################################
126# Next, you have to give a upper boundary for the number of iterations (int)
127# NOTE:
128# If it is set to zero, no inverse modelling is done, but coverages
129# (resolution, variogram, etc..) may be calculated.
130# This is especially useful in conjunction with a valid prior/starting model!
131#########################################################################################
13220
133#########################################################################################
134# The next (logical) switch (ldc) controls whether we invert for COMPLEX (EIT, ldc = F)
135# or REAL values (ERT) (ldc = T)
136#########################################################################################
137F
138#########################################################################################
139# (logical) switch (lrobust) for robust inversion (e.g. La Breque et al 1996)
140#########################################################################################
141F
142#########################################################################################
143# Do you want a Final phase improvement (FPI) ? set (lfphai) the next logical to T
144# NOTE:
145# If (ldc == .FALSE. .and. lfphai == .TRUE.) lelerr = .FALSE. (error ellipses)
146# This has the impact, that no error ellipses are used in FPI.
147##
148# However, this may be overwritten by setting mswitch = mswitch + 32 in the first line !!
149#########################################################################################
150T
151#########################################################################################
152# The next two floats determine the error model for resistance/voltage
153# which is currently implemented as \delta R = A * abs(R) + B
154# Thus, A gives the relative error estimate [%] and B gives the absolute error estimate.
155#
156# NOTE:
157# The first (A) Parameter also controls whether or not to couple the (maybe COMPLEX)
158# error model to any noise additions (Yes, voltages in CRTomo can be noised...)
159# If A is set to -A , the whole error model is taken as noise model.
160# Giving this, you may want to add an ensemble seed number, which may be crucial for
161# any kind of monte carlo study, at the end of this crt-file..
162# The noise is also written to the file 'crt.noisemod' which may be changed afterwards if
163# you like to decouple error and noise model.
164# NOTE:
165# CRTomo is looking for crt.noisemod in the current directory as default.
166# If it is existing or a valid file, it gives a note about this and
167# trys to get a noise model from the data contained
168#########################################################################################
169-1.0
170#########################################################################################
171# Error model parameter B [Ohm]
172#########################################################################################
1731e-3
174#########################################################################################
175# Next 4 (float) numbers control the phase error model as can be found in
176# Flores-Orozsco et al, 2011
177# \delta \phi = A1*abs(R)^B1 + A2*abs(pha) + p0
178###
179# A1 [mrad/Ohm/m]
180#########################################################################################
1810.0
182#########################################################################################
183# B1 []
184#########################################################################################
1850.0
186#########################################################################################
187# A2 [%]
188#########################################################################################
1890.0
190#########################################################################################
191# p0 [mrad]
192#########################################################################################
193#########################################################################################
194# If you use FPI, note that if P0 is set to a negative value, the phase model is set
195# to a homogenous model if FPI starts, this was used by AK as default...
196# the p0 is set to its positive value for error calc, if this is used (of course..)
197#########################################################################################
198#########################################################################################
1991e-1
200#########################################################################################
201# Here you can decide if you want a homogenous starting model (overwritten with prior)
202# logical (lrho0) for both, magnitude and phase
203#########################################################################################
204T
205#########################################################################################
206# homogenous background resistivity value for magnitude [Ohm m]
207#########################################################################################
208100.00
209#########################################################################################
210# homogenous background value for the phase [mrad]
211#########################################################################################
2120.000
213#########################################################################################
214# Some people prefer having one crt-file for many inversions.
215# If you set this logical T, CRTomo tries to read in another crt-style file after
216# the first inversion was done.
217# This also means, that any data arrays (memory model!!) are reallocated and thus
218# different grids/electrodes/measurements can be given to CRTomo...
219#########################################################################################
220F
221#########################################################################################
222# Dimensionality switch (integer) to control whether or not to have a _real_ 2D (=0)
223# or a 2.5D (=1) forward solution. 2.5D assumes a 3D model space with a resistivity
224# distribution that is homogeneous in the y direction.
225# NOTE:
226# If you like to have a true 2D (i.e. setting to 0) you have to keep in mind that
227# the sink node setting (down below) has to be set.
228# Also note that if 2D mode is selected the singularity removal switch may be helpful to
229# reduce numerical issues.
230#########################################################################################
2311
232#########################################################################################
233# (logical) switch whether to introduce a fictitious sink node (sink is here in the sense
234# of a -I electrode at some place in b by solving Ax=b with Cholesky
235#########################################################################################
236F
237#########################################################################################
238# Node number (int) of the sink node
239# The chosen node should conform to the following properties:
240# - not a boundary node
241# - not an electrode
242# - should be positioned at the center of the grid with a preferably large distance to
243# all electrodes
244#########################################################################################
2450
246#########################################################################################
247# Do you like to read in some boundary potential values ? (logical)
248# The boundary values are helpful for tank experiments at known voltages (i.e.
249# inhomogenous Dirichlet boundaries)
250#########################################################################################
251F
252#########################################################################################
253# Path to the boundary values, blanks can be included
254#########################################################################################
255empty
256#########################################################################################
257# In some older cfg files, this would be the end of the cfg-file.
258# Yet, to control regularization you can give in the next line an integer (ltri) to
259# manage it:
260# (=0) - Smooth regularization for regular grids only (Nx and Nz have to be correct!!)
261# (=1) - Smooth triangular regularization (should be used as default and the method
262# of choice
263# (=2) - Smooth triangular regularization, second order (not yet implemented..)
264# (=3) - Levenberg damping (i.e. C_m^-1 = lambda * I)
265# (=4) - Marquardt-Levenberg damping (i.e. C_m^-1 = lambda * diag{A^T C_d^-1 A} )
266# (=5) - MGS regularization (pure MGS after Zhdanov & Portniaguine):
267# C_m^-1 \approx \int \frac{(\nabla m_{ij})^2}{(\nabla m_{ij})^2+\beta^2}\;dA
268# (=6) - MGS with sensitivity weighted beta: = beta / f_{ij} (from Blaschek 2008)
269# where f_{ij} = (1 + g(i) + g(k))^2 and g(i,k) = log_{10} coverage (m_{i,k})
270# (=7) - MGS with sensitivity weighted beta (as with 6) but normalized:
271# f_{ij} = ((1 + g(i) + g(k))/mean{coverage})^2
272# (=8) - MGS as in 6, but here a modified version of Roland Blaschek (which I apparently
273# didn't understood, but was given to me from Fred...).
274# For more details please have a look into bsmatm_mod.f90 -> SUBROUTINE bsmamtmmgs
275# (=9) - Same as 8, but with mean coverage normalization
276# (=10) - Total variance (TV) regularization (not well tested, but I think it is BETA)
277#
278# NOTE:
279# For MGS and TV you can specify a beta-value (0<beta<1) in this cfg!
280#
281# (=15) - Stochastic regularization. Here, C_m is a full matrix which needs to be
282# inverted at the beginning of the inverse process. For this regu you have to
283# specify a proper integral scale and covariance function (see Nx-switch).
284# (>15) - not allowed
285# (+32) - Fix lambda value to a given value (1 as default)
286# The switch is binary tested so it is as cumulative as mswitch.
287# Also it is removed after a internal logical was set true (llamf).
288# The lambda value can be given in a additional line after the ltri value.
289#
290# NOTE:
291# The order of the additional switches (fixed lambda, beta, seed) is treated like:
292# - fixed lambda
293# - MGS/TV beta
294# - Random seed
295# Each in a seperate line!
296#########################################################################################
2971
298#########################################################################################
299# The following line depends on the previous choice you made, so it may be the Random
300# seed, the fixed lambda value or the MGS/TV beta.
301# In case of an error (fixed format integer read!) this line is just omitted.
302#
303# NOTE:
304# For people with cfg-files with more than one inversion run (another data set = T), the
305# next line should contain the beginning of the next cfg.
306#########################################################################################
307lam/beta/seed
..note
The crtomo.cfg file is imported in the **rall.f90** file
MGS¶
Allerdings könnte die beta Bestimmung etwas zeitaufwendig sein, daher sollte MGS mehr oder weniger als post-alpha Stadium bezeichnet werden.
Unterstützt werden für diesen Integer am Ende vom crtomo.cfg-file die Zahlen 5,6 & 7. Daran anschließend kann man noch ein beta angeben, sodass das cfg file in etwa so aussieht:
------ schnip ------------
F ! fictitious sink ?
1660 ! fictitious sink node number
F ! boundary values ?
boundary.dat
6 ! regularization switch
0.01 ! MGS beta
5 ist identisch zu dem Ansatz von Zhdanov [2002], Geophysical Inverse Theory and Regularization Problems, Elsevier.
6 & 7 sind im Grunde die von Blaschek et al. 2008, wobei hier ein Bug von Roland gefixt wurde der mit dem update der Sensitivität und des Modells nach jedem update zu tun hatte (im Grunde wurde die Glättung nicht wieder neu berechnet was nicht ganz korrekt ist).
Note
!!! Important !!! Man kann diese Glättung aber auch fixen, wenn man das unbedingt will. Dann wird die MGS-Glättung vom Startmodell genommen, welches in der Regel ja noch keine Struktur hat. Realisiert wird dies in dem man das MGS-beta auf einen _negativen_ Wert setzt.
crmod.cfg¶
The file is structured as follows. It is the configuration file of CRMod.
1 ***FILES***
2 ../grid/elem.dat
3 ../grid/elec.dat
4 ../rho/rho.dat
5 ../config/config.dat
6 F
! potentials ?
7 ../mod/pot/pot.dat
8 T
! measurements ?
9 ../mod/volt.dat
10 F
! sensitivities ?
11 ../mod/sens/sens.dat
12 F ! another dataset ?
13 1 ! 2D (=0) or 2.5D (=1)
14 F ! fictitious sink ?
15 1660 ! fictitious sink node number
16 F ! boundary values ?
17 boundary.dat
18 ! optional integer switch
Line 1: Not used
Line 2: Absolute or relative path to grid (
elem.dat) fileLine 3: Absolute or relative path to electrode (
elec.dat) fileLine 4: Absolute or relative path to parameter (
rho.dat) fileLine 5: Absolute or relative path to electrode configuration (
config.dat) fileLine 6: Switch enabling (T) or disabling (F) output of potentials for the measurement configurations.
Line 7: Filename prefix for potentials. A four digit number will be appended.
Line 8: Switch to enable (T) or disable (F) output of voltages.
Line 9: Filename of voltages for all measurement configurations.
Line 10: Switch to enable (T) or disable (F) output of sensitivities.
Line 11: Filename prefix for sensitivity files.
Line 12: Set either to T in case another configuration file (Lines 1 - 18) is appended to this file (Lines 19+), or F if the configuration file consist only of 18 lines.
Line 13: Assume a 2D (0) or a 2.5D (1) subsurface
Line 14: Use a fictitious sink (T/F)
Line 15: Node number of fictitious sink
Line 16: Use user supplied boundary values (T/F)
Line 17: Filename of the boundary values
Line 18: Optional integer switch:
+1: Enable analytical solution (lana)
+2: Modelling with K-factor (wkfak)
+4: Singularity removal (lsr). Please note that this option can’t be used in conjunction with the analytical solution.
crmod.pid¶
The file contains the process ID number, like in
ps -a
pidof CRTomo
decouplings.dat¶
Decoupling for triangular smooth cell interfaces can be done using this file. The first line contains the number of decouplings, and the subsequent lines contain one decoupling each. One decoupling consists of two integer numbers of the adjoining element cells, and one floating point value which determines the decoupling factor to be multiplied to the original regularisation. A value of 0 completely decouples the regularisation of a given interface, while a value of one does not change anything. Values larger than 1 increase the regularisation above the norm.
Example:
3
3 4 0.0
5 8 0.5
8 10 0.0
The numbering is independent of the application of the CutMcK algorithm to a given grid. Use the order of appearance in the elem.dat file for the numbering.
sens.dat¶
Each sens.dat contains the modelled sensitivity distribution for the
corresponding measurement configuration defined in config.dat, i.e. the
(consecutive) number in the file name corresponds to the line number in
config.dat.
The modelled sensitivity is given by \(\frac{\partial V_i}{\partial
\sigma_j} \left[\frac{V\ m}{S}\right]\), where \(V_i\) is the voltage (in
\(V\)) of the \(i\)-th measurement (assuming a unit current of 1
\(A\)), and #:math:j is the conductivity (inverse of resistivity) (in
\(S/m\)) of the \(j\)-th element (of type 8). The first line in
sens.dat contains the integrated sensitivity value \(\sum_j
\frac{\partial V_i}{\partial \sigma_j}\).
The format of sens.dat is explained by means of an example file:
1.3385538 3140.5132
-13.399500 -0.25000000 7.50053499E-04 -8.15268550E-07
-7.1114998 -0.25000000 1.99041306E-03 -1.93495089E-06
-3.6995001 -0.25000000 3.69597459E-03 -3.32863351E-06
...
...
...
38.699501 -20.442499 1.44582140E-04 5.84734394E-08
42.111500 -20.442499 1.98332040E-04 -8.41067092E-08
48.399502 -20.442499 2.44848023E-04 -4.05481018E-07
- Line 1:
The first number denotes the absolute value of the sum of sensitivities (\(abs(\sum s_{ij}\)).
The second number denotes the phase value of the sum of sensitivities in mrad (\(1000 \cdot atan(Im(\sum(s_{ij})) / Re(\sum s_{ij})))\)).
- Line 2:
Column 1 and 2: Centered (x,z) coordinates for the element
Column 3 and 4: Real and Imaginary parts of sensitivity
Plotting
Plotting of sensitivity files can be accomplished using the crlab_py python
library:
from crlab_py.mpl import *
import crlab_py.elem as elem
import numpy as np
if __name__ == '__main__':
elem.load_elem_file('elem.dat')
elem.load_elec_file('elec.dat')
indices = elem.load_column_file_to_elements_advanced('sens0009.dat', [2,3], False, False)
elem.plt_opt.title = ''
elem.plt_opt.cblabel = r'fill'
elem.plt_opt.reverse = True
elem.plt_opt.cbmin = -1
elem.plt_opt.cbmax = 1
elem.plot_elements_to_file('sensitivity_1.png', indices[0], scale='asinh')
elem.plot_elements_to_file('sensitivity_2.png', indices[1], scale='asinh')
The scale-setting enables a special data transformation to plot positive and negative values over a large value range. The inverse sinus hyperbolicus shows a nearly linear behaviour between -1 and 1. Outside of this interval it shows behaviour roughly similar to the logarithm (but not the same!):
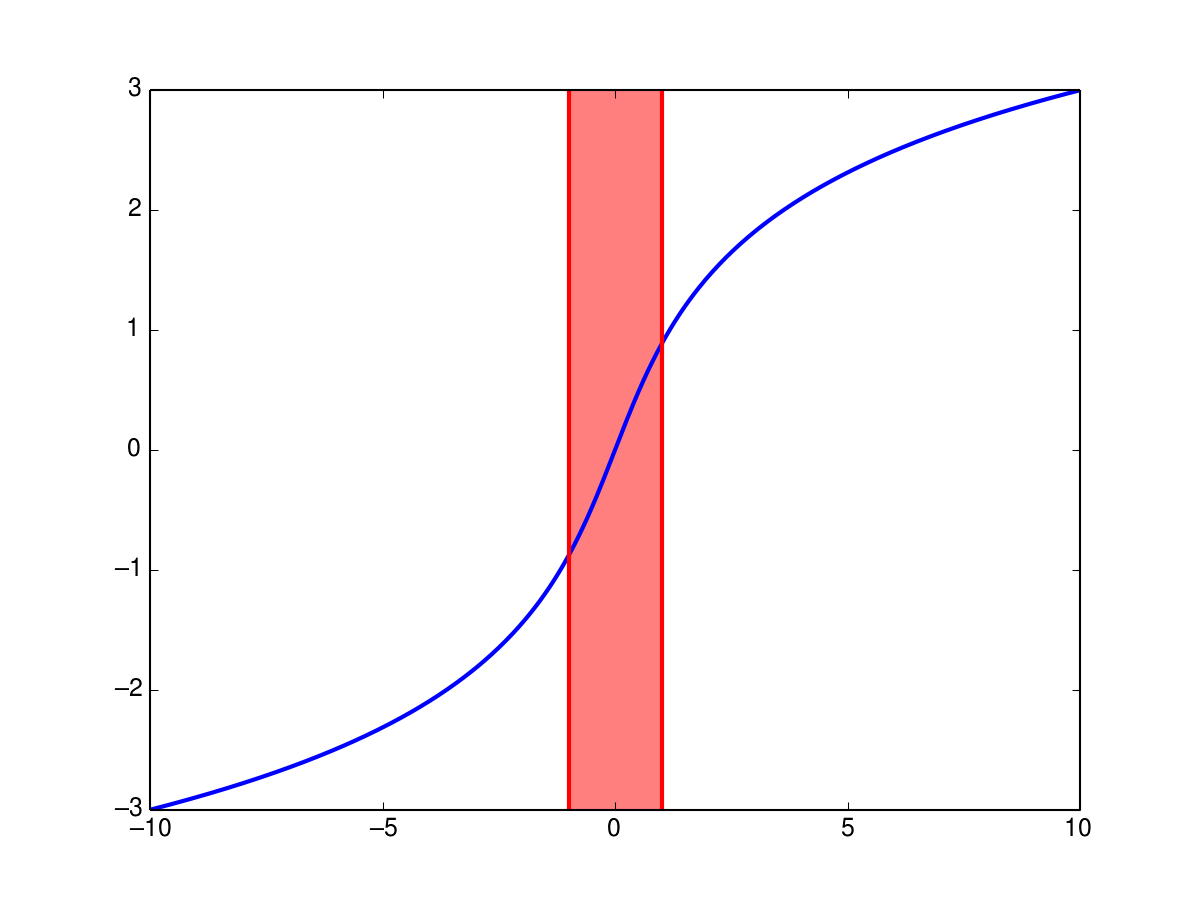
The sensitivities \(s_{ij}\) are transformed according to the formula:
The factor dyn ensures that all sensitivity values are transformed to the
value interval \(]-1,1[\). Therefore, all of them lie in the logarithmic’
range of the asinh function. All `s_{ij} values are normed to within the range
\([0,1]\) using the factor norm. The term in the arcsin-function can
thus not get larger than \(10^{\text{dyn}}\) and can be normed using the
arcsinh term in the denominator.
Warning
Always provide, or at least mention, the asinh transformation when presenting sensitivity plots. Also the normalization factor norm should be provided.
inv.elecpositions¶
When CRTomo is called it writes the electrode positions (as read from elem.dat
and elec.dat) to this file. The first line contains the number of (recognized)
electrodes, and each of the following lines contains two numbers: The x and z
coordinate of the corresponding electrode.
38
2.0000000000000000 -3.0000000000000000
6.0000000000000000 -3.0000000000000000
10.000000000000000 -3.0000000000000000
...
...
...
18.000000000000000 -37.000000000000000
22.000000000000000 -37.000000000000000
26.000000000000000 -37.000000000000000
inv.gstat¶
Created when CRTomo is called. Contains various grid statistics.
Regular grid:
Grid statistics:
Gridcells: 9360
ESP Min/Max: 0.5000 0.5000
GRID Min/Max: 0.5000 82.9247
GRID-x Min/Max: 0.5000 29.5000
GRID-y Min/Max: 0.5000 77.5000
Mean/Median/Var: 0.5000 0.5000 0.0000
inv.lastmod¶
For DC/complex inversion: Holds the (relative) path to the final iteration’s .mag file
For FPI: Holds the (relative) path to the FPI final iteration’s .mag file
inv.lastmod_rho¶
Only created if FPI is used: Holds the (relative) path to the final iteration’s .mag file of the complex inversion.
grid/¶
elec.dat¶
elec.dat contains the electrode information, i.e. the numbers of nodes
where electrodes are located (the node position is determined in elec.dat). The
format of elec.dat is explained by means of an example file:
36
962
964
...
2788
2870
2952
Line 1: Number of electrodes.
Line 2-End: Node numbers (as defined in
elem.dat) where electrodes are located.
elem.dat¶
elem.dat contains all necessary information on the finite-element
discretization to be used, including the position and numbering of nodes which
constitute individual elements. The format of elem.dat is explained in the
following by means of an example file (Line numbers are prefixed in each
line):
{\tiny
\begin{verbatim}
1 861 3 42
2 8 800 4
3 12 40 2
4 11 80 2
5 1 -7.5 0
...
...
...
865 861 22.5 -12.5
866 42 43 2 1
...
...
...
1665 860 861 820 819
1666 1 2
...
...
...
1705 40 41
1706 41 82
...
...
...
1785 42 1
1786 1
...
...
...
1905 1
\end{verbatim}
}
- Line 1:
First column: Number of nodes
Second column: Number of element types
Third column: Bandwidth of the resulting finite-element matrix
Line 2-4: For each element type (in this example there are three: 8 (rectangles), 11 (Mixed), 12 (Neumann)), list the following:
First column: Element type
Second column: Number of elements for this type
Third column: Numnber of element this type has. Elements with 2 nodes are called degenerated
- Lines 5 - 865: Node coordinates. 3 Columns:
1 Node number: Internal Finite-Element number for this node. 2 X-coordinate 3 Z-coordinate (positive direction: upwards)
Lines 866 - 1665: Nodes of the first element type. In this case four nodes define one rectangular cell.
Lines 1666 - 1705: Nodes of second element type. In this case two nodes define a boundary condition of type 12 (Neumann).
Lines 1706 - 1785: Nodes of second element type. In this case two nodes define a boundary condition of type 11 (Mixed).
Lines 1786 - 1905: Number of the element of type 8 adjacent to the boundary elements (in the order of previous appearance).
Notes:
Elements need to be defined counter-clockwise
Boundary elements are defined from left to right (clockwise!)
The bandwith of the resulting finite-element matrix, the last entry in line 1 of elem.dat, is given by one plus the occurring maximal difference between the numbers of any two nodes belonging to the same element. It is thus dependent on the employed numbering of nodes.
In the present CRMod version, only elements of type 8 (quadrangular element composed of four triangular elements) and boundary elements of type 12 (homogeneous Neumann boundary condition; to be used at the Earth’s surface or at boundaries of a confined tank) or type 12 (mixed, or absorbing, boundary condition; to be used at boundaries within a half or full space) are supported.
In elem.dat, boundary elements must be listed after the normal (areal)
elements. Along the edges of elements, a linear behaviour of the electric
potential is assumed. Although elements may exhibit an irregular shape,
elements with acute angles should be avoided.
Note
New regular grids (elem.dat and elec.dat) can be created using Griev!
inv/¶
cjg.ctr¶
For each iteration, save the residuum of each Conjugate Gradient step. The
number of CG-steps can also be found in the inv.ctr file for each
iteration.
coverage.mag¶
L1 data-weighted cumulated sensitivity (normalized)
\(S_i^{L1} = \sum_j^N \frac{|\partial V_j|}{\epsilon_i |\partial \rho_i|}\)
2880 874956.88680652122
0.25000000000000000 -0.25000000000000000 -0.55853918225079879
0.75000000000000000 -0.25000000000000000 -0.28004078693583917
...
1.2500000000000000 -0.25000000000000000 -0.12203557213931025
1.7500000000000000 -0.25000000000000000 -0.14832386170628217
First row:
First column: number of sensitivity values to follow
Second column: Maximum sensitivity (linear value), used to normalize values down below.
All following rows:
First column: Central x-coordinate of cell
Second column: Central z-coordinate of cell
Third column: \(log_{10}\left( \frac{S_{ij}}{S_{ij}^{max}}\right)\) (Normalized log10 of summed sensitivities)
As the third column is \(log_{10}\), only negative or zero values can be expected (0-1).
Note
Computed in bbsens.f90
coverage.mag.fpi¶
Contains the coverage (L1) of the sensitivties used in the FPI (thus only updating the phase component of the complex resistivity) for the final model.
The structure of the file can be found in the preceding section
(coverage.mag).
ata.diag¶
L2 data-weighted cumulated sensitivity (normalized), d_i
\(S_i^{L2} = \sum_j^N \frac{|\partial V_j|^2}{\epsilon_i |\partial \rho_i|^2}\)
2880 27.3748341 2.93462502E+09
397261824. -0.868474960
1.72104538E+09 -0.231760025
...
2.93462502E+09 0.00000000
2.03916826E+09 -0.158099174
First line holds three columns:
number of sensitivity values (equal to number of mesh cells)
minimum of d_i (i.e., of the first column of all following rows)
maximum of d_i (i.e., of the first column of all following rows)
All following rows:
First column: Diagonal entry of \(A^T C_d^{-1} A\): d_i
Second column: \(log_{10} \left(\frac{d_i}{d_{max}}\right)\)
As the second column contains only \(log_{10}\) values only negative or zero values can be expected (i.e. values in the range between zero and one).
With \(C_d{^-1} = W_d^T W_d\); \(W_d = diag \left(\frac{1}{\epsilon_1}, \ldots, \frac{1}{\epsilon_n} \right)\)
Note
Computed in bmcm_mod.f90 function bata
ata_reg.diag¶
First column: Diagonal entry of \(A^T C_d^{-1} A + C_m^{-1}(\lambda)\): \(d_i\)
Second column: \(log_{10} \left(\frac{d_i}{d_{max}}\right)\)
Question: In what way are these values normalized?
cov1_m.diag and cov2_m.diag¶
Cov1: \(\left[A^T C_d^{-1} A + C_m^{-1}(\lambda) \right]^{-1}\)
Cov2: \(\left[A^T C_d^{-1} A + C_m^{-1}(\lambda) \right]^{-1} A^T C_d^{-1} A \left[A^T C_d^{-1} A + C_m^{-1}(\lambda) \right]^{-1}\)
What can I do with these files?
Both files have the format:
std err (%) | \(\delta(\sigma')\) | \(\delta(\sigma'')\)
In order to get an absolute uncertainty for a given paramter (magnitude AND phase), use the formula:
\(\delta Parameter = Parameter \cdot \frac{std err}{100}\)
For more information have a look at the ModelProbe documents D2.1.2_UBO.pdf and M2.2_UBO.pdf, which can be found in the CRTomo repository.
Examples can also be found in the examples/ subdirectory of the CRTomo repository.
res_m.diag¶
Stores the resolution matrix, computed from the last iteration. This file is written if the value 4 is added to the mswitch. Resolution matrix:
\(\left[A^T C_d^{-1} A + C_m^{-1}(\lambda) \right]^{-1} A^T C_d^{-1} A\)
the first row has four columns:
number of values (cells)
lambda that R was computed for
min R value
max R value. This is the value used to normalize the data
second to last row:
first column linear value, NOT normalized
second column: \(log_{10}\) value, normalized to [0, 1].
No units [1].
Note
For further information, have a look at the CRTomo source file bmcm_mod.f90 in SUBROUTINE bres.
eps.ctr¶
This file consists of two parts: The first part describes the errors in
relation to the measurements (volt.dat). The second one describes the
errors for each iteration in relation to the forward solution of the current
model space.
{\tiny
\begin{verbatim}
1 1/eps_r 1/eps_p 1/eps eps_r eps_p eps -log(|R|) -Phase (rad)
2 14.2 20000.0 14.2 0.703E-01 0.500E-04 0.703E-01 -3.553902 0.1322917E-02
...
...
...
527 6.0 20000.0 6.0 0.167 0.500E-04 0.167 2.276732 0.3437240E-03
528
529 IT# 0
530 eps psi pol Re(f(m)) Im(f(m))
531 0.395 2.342500 1 0.2532884 0.000000
...
...
...
1056 0.718E-01 5.259448 1 -3.666626 0.000000
1057
1058 IT# 1
1059 eps psi pol Re(f(m)) Im(f(m))
1060 0.395 1.881460 1 0.4353101 0.8566426E-02
...
...
...
1585 0.718E-01 0.509647 1 -4.007404 0.5183748E-02
1586
1587 IT# 2
1588 eps psi pol Re(f(m)) Im(f(m))
1589 0.395 1.898024 1 0.4287698 0.8681247E-02
...
...
...
2114 0.718E-01 0.418030 1 -4.013978 0.5163230E-02
2115
2116 PIT# 2
2117 eps psi pol Re(f(m)) Im(f(m))
2118 0.371E-02 0.491851 1 0.4287698 0.8681247E-02
...
...
...
2643 0.305E-02 0.050550 1 -4.013978 0.5163230E-02
2644
2645 PIT# 3
2646 eps psi pol Re(f(m)) Im(f(m))
2647 0.371E-02 0.159764 1 0.4287700 0.6262148E-02
...
...
...
3172 0.305E-02 0.409256 1 -4.013978 0.6258056E-02
3173
3174 PIT# 4
3175 eps psi pol Re(f(m)) Im(f(m))
3176 0.371E-02 0.160427 1 0.4287700 0.6259686E-02
...
...
...
3701 0.305E-02 0.409742 1 -4.013978 0.6259539E-02
\end{verbatim}
}
Line 1: Header for the raw data description. \(eps\) is the complex error which, depending on the use of the error ellipsis, is based on both magnitude and phase errors (Error ellipsis, \(eps = \sqrt{(eps_r)^2 + (eps_p)^2}\)), or only the magnitude error (no error ellipsis, \(eps = eps_r\)). datum(Re, Im) denotes the real and imaginary parts of the measurements as stored internally in CRTomo:
\(Re(datum) = -log_e(|R|)\) (Note the natural logarithm!) and \(Im(datum) = - Phase (rad)\). \(eps_r\) is the magnitue error (logarithm) and eps_p is the phase error (rad). \(eps\) is used in the complex inversion while \(eps_p\) is used in the final phase improvement.
\(eps_r\) and \(eps\) can directly be compared to \(log_e(|R|)\) and \(eps_p\) can be compared to \(Phase (rad)\).
Lines 2 - 527: Error descriptions for each measurement.
Line 529: Indicates the Iteration the following data describes.
Line 530: Header for the iteration descriptions. \(eps\) is the complex error. \(psi = \frac{d_i - f_i}{\epsilon_i}\) is the error weighted residuum of the data \(d_i\) and the forward response of the current iteration \(d_i\). \(pol\) gives the polarity of the measurements, \(d\) is the forward solution, and \(f\) is the measurement.
inv.ctr¶
The inv.ctr file contains all information related to the inversion results.
As such it is the most important file to assess and improve inversion results.
In the following certain parts of the file will be explained:
Lines 1 to 10 hold information regarding the specific CRTomo version that was used in the inversion.
Lines 11 to 44 repeat the legacy parameters of the crtomo.cfg file.
Lines 46 to 55 contain information of the grid used and the artificial noise applied to the data.
Lines 57 to 73 show information regarding all regularization options that can be controlled.
Lines 75 to 87 hold various options.
Lines 89 to 101 contain fixed constants that are hardwired into the CRTomo code.
Line 103 separates information available before the inversion from inversion regarding the inversion process.
Line 105 contains a header which describes all columns to follow.
Lines 107 to 174 contain information of the complex inversion.
Lines 178 to 195 contain information of the final phase improvement.
Line 196 indicates that the inversion finished gracefully.
{\tiny
\begin{verbatim}
1 ##
2 ## Complex Resistivity Tomography (CRTomo)
3 ##
4 ## Git-Branch master
5 ## Git-ID 334c078edcdc3b010a9cd68c07880ae845795c2f
6 ## Compiler ifort
7 ##
8 ## Created Tue-Oct-18-14:36:17-2011
9 ##
10
11 1 # mswitch
12 ../grid/elem.dat
13 ../grid/elec.dat
14 ../mod/volt.dat
15 ../inv
16 F ! difference inversion or (m - m_{prior})
17
18
19
20 ***PARAMETERS***
21 0 ! nx-switch or # cells in x-direction
22 -1 ! nz-switch or # cells in z-direction
23 1.0000 ! smoothing parameter in x-direction
24 1.0000 ! smoothing parameter in z-direction
25 20 ! max. # inversion iterations
26 F ! DC inversion ?
27 T ! robust inversion ?
28 T ! final phase improvement ?
29 5.0000 ! rel. resistance error level (%) (parameter A1 in err(R) = A1*abs(R) + A2)
30 0.10000E-03 ! min. abs. resistance error (ohm) (parameter A2 in err(R) = A1*abs(R) + A2)
31 0.0000 ! phase error model parameter A1 (mrad/ohm^B) (in err(pha) = A1*abs(R)**B + A2*abs(pha) + A3)
32 0.0000 ! phase error model parameter B (-) (in err(pha) = A1*abs(R)**B + A2*abs(pha) + A3)
33 0.0000 ! phase error model parameter A2 (%) (in err(pha) = A1*abs(R)**B + A2*abs(pha) + A3)
34 2.5000 ! phase error model parameter A3 (mrad) (in err(pha) = A1*abs(R)**B + A2*abs(pha) + A3)
35 T ! homogeneous background resistivity ?
36 40.000 ! background magnitude (ohm*m)
37 0.0000 ! background phase (mrad)
38 F ! Another dataset?
39 0 ! 2D (=0) or 2.5D (=1)
40 T ! fictitious sink ?
41 4647 ! fictitious sink node number
42 F ! boundary values ?
43 boundary.dat
44 1
45
46 ***Model stats***
47 # Model parameters 9360
48 # Data points 535
49 Add data noise ? F
50 Couple to Err. Modl? T
51 seed 1
52 Variance 0.0000
53 Add model noise ? F
54 seed 0
55 Variance 0.0000
56
57 ******** Regularization Part *********
58 Prior regualrization F
59 Regularization-switch 1
60 Regular grid smooth F
61 Triangular regu T
62 Triangular regu2 F
63 Levenberg damping F
64 Marquardt damping F
65 Minimum grad supp F
66 MGS beta/sns1 (RM) F
67 MGS beta/sns2 (RM) F
68 MGS beta/sns1 (RB) F
69 MGS beta/sns2 (RB) F
70 TV (Huber) F
71 Stochastic regu F
72 Fixed lambda? F
73 Taking easy lam_0 : 9360.000
74
75 ******** Additional output *********
76 mswitch 1
77 Read start model? F
78 Write coverage? T
79 Write MCM 1? F
80 Write resolution? F
81 Write MCM 2? F
82 Using Gauss ols? F
83 Forcing negative phase? F
84 Calculate sytop? T
85 Verbose? F
86 Error Ellipses? F
87 Restart FPI with homogenous phase? F
88
89 ***FIXED***
90 -- Sytop [m] : -39.000
91 Force negative phase ? F
92 Ratio dataset ? F
93 Min. L1 norm 1.0000
94 Min. rel. decrease of data RMS : 0.20000E-01
95 Min. steplength : 0.10000E-02
96 Min. stepsize (||\delta m||) : 0.0000
97 Min. error in relaxation : 0.10000E-03
98 Max. # relaxation iterations : 936
99 Max. # regularization steps : 30
100 Initial step factor : 0.50000
101 Final step factor : 0.90000
102
103 -------------------------------------------------------------------------------------------------------------
104
105 ID it. data RMS stepsize lambda roughn. CG-steps mag RMS pha RMS - # data L1-ratio steplength
106
107 *************************************************************************************************************
108 IT 0 7.632 7.630 3.887 0 1.13
109 *************************************************************************************************************
110 UP 1 2.874 736. 9360. 0.1551 226 1.000
111 UP 2 2.429 731. 4680. 0.3507 179 1.000
112 UP 3 2.044 726. 2569. 0.6208 143 1.000
113 UP 4 1.762 723. 1553. 0.9112 117 1.000
114 UP 5 1.573 723. 1020. 1.183 100 1.000
115 UP 6 1.448 725. 713.1 1.424 89 1.000
116 UP 7 1.363 726. 522.3 1.637 80 1.000
117 UP 8 1.302 728. 395.7 1.833 73 1.000
118 UP 9 1.258 730. 307.4 2.016 67 1.000
119 UP 10 1.223 731. 243.5 2.194 60 1.000
120 UP 11 1.196 733. 195.9 2.368 55 1.000
121 UP 12 1.174 735. 159.6 2.543 51 1.000
122 UP 13 1.155 735. 131.3 2.732 45 1.000
123 UP 14 1.139 734. 109.1 2.932 39 1.000
124 UP 15 1.126 735. 91.30 3.123 36 1.000
125 UP 16 1.115 736. 76.90 3.321 33 1.000
126 UP 17 1.105 737. 65.12 3.543 30 1.000
127 UP 18 1.095 738. 55.43 3.786 28 1.000
128 UP 19 1.087 737. 47.42 4.049 25 1.000
129 UP 20 1.078 737. 40.74 4.324 23 1.000
130 UP 21 1.071 736. 35.15 4.639 21 1.000
131 UP 22 1.064 736. 30.45 4.973 20 1.000
132 UP 23 1.058 736. 26.48 5.331 19 1.000
133 UP 24 1.052 734. 23.10 5.715 18 1.000
134 UP 25 1.047 736. 20.21 6.091 18 1.000
135 UP 26 1.042 737. 17.73 6.491 18 1.000
136 UP 27 1.037 737. 15.59 6.913 18 1.000
137 UP 28 1.030 735. 13.76 7.422 17 1.000
138 UP 29 1.026 736. 12.18 7.897 17 1.000
139 UP 30 1.023 737. 10.80 8.405 17 1.000
140 UP 31 3.409 368. 12.18 1.974 17 0.500
141 *************************************************************************************************************
142 IT 1 1.026 736.3 12.18 7.897 17 1.235 0.9566 0 1.23 1.000
143 *************************************************************************************************************
144 UP 0 0.5746 22.2 12.18 6.673 43 1.000
145 UP 1 0.5989 22.8 18.42 5.641 46 1.000
146 UP 2 0.6257 24.6 27.23 4.841 46 1.000
147 UP 3 0.6546 27.7 39.28 4.211 51 1.000
148 UP 4 0.6850 31.5 55.25 3.718 54 1.000
149 UP 5 0.7160 35.8 75.79 3.333 56 1.000
150 UP 6 0.7479 40.5 101.4 3.023 57 1.000
151 UP 7 0.7807 45.3 132.5 2.771 58 1.000
152 UP 8 0.8144 50.2 169.0 2.560 59 1.000
153 UP 9 0.8494 55.2 210.5 2.379 61 1.000
154 UP 10 0.8853 60.1 256.1 2.222 63 1.000
155 UP 11 0.9212 64.9 304.5 2.087 66 1.000
156 UP 12 0.9564 69.4 354.2 1.970 67 1.000
157 UP 13 0.9899 73.5 403.4 1.871 68 1.000
158 UP 14 1.021 77.3 450.8 1.787 69 1.000
159 UP 15 0.7534 36.8 403.4 3.787 68 0.500
160 *************************************************************************************************************
161 IT 2 0.6577 3.546 403.4 7.405 68 1.238 0.9554 0 0.048
162 *************************************************************************************************************
163 UP 0 0.9914 66.8 403.4 1.866 68 1.000
164 UP 1 1.022 70.3 450.4 1.783 69 1.000
165 UP 2 0.7629 33.4 403.4 3.640 68 0.500
166 *************************************************************************************************************
167 IT 3 0.9914 66.77 403.4 1.866 68 1.528 0.9726 0 1.000
168 *************************************************************************************************************
169 UP 0 1.008 0.152 403.4 1.812 69 1.000
170 UP 1 0.9788 0.201 361.5 1.893 78 1.000
171 UP 2 0.9994 0.761E-01 403.4 1.837 69 0.500
172 *************************************************************************************************************
173 IT 4 1.000 0.8132E-01 403.4 1.835 69 1.536 0.9723 0 0.534
174 *************************************************************************************************************
175
176 -----------------------------------------------------------------------------------------------------------------
177
178 *************************************************************************************************************
179 PIT 4 0.9723 1.536 0.9723 0
180 *************************************************************************************************************
181 PUP 1 0.9305 0.798E-02 9360. 0.1051E-02 26 1.000
182 PUP 2 0.9263 0.144E-01 4680. 0.1684E-02 30 1.000
183 PUP 3 0.9305 0.798E-02 9360. 0.1051E-02 26 1.000
184 PUP 4 0.9348 0.438E-02 0.1808E+05 0.7200E-03 25 1.000
185 PUP 5 0.9391 0.241E-02 0.3373E+05 0.5406E-03 28 1.000
186 PUP 6 0.9437 0.134E-02 0.6071E+05 0.4388E-03 32 1.000
187 PUP 7 0.9489 0.774E-03 0.1053E+06 0.3719E-03 42 1.000
188 PUP 8 0.9560 0.526E-03 0.1749E+06 0.3192E-03 50 1.000
189 PUP 9 0.9656 0.587E-03 0.2746E+06 0.2747E-03 62 1.000
190 PUP 10 0.9772 0.952E-03 0.3992E+06 0.2385E-03 70 1.000
191 PUP 11 0.9888 0.151E-02 0.5297E+06 0.2118E-03 74 1.000
192 PUP 12 0.9985 0.207E-02 0.6415E+06 0.1943E-03 83 1.000
193 *************************************************************************************************************
194 PIT 5 0.9888 0.1509E-02 0.5297E+06 0.2118E-03 74 1.536 0.9888 0 1.000
195 *************************************************************************************************************
196 ***finished***
\end{verbatim}
}
.modl files¶
The first row contains the number of grid cells (conductivities). Starting with the second row, the magnitude (in \(\Omega m\)) and the phase (in \(mrad\)) are displayed for each grid cell.
.mag files¶
The first row again contains the number of grid cells along with the normalized magnitude or phase misfit for the current inversion iteration. The following rows contain the x and z centroid coordinates and the magnitude (in \(\Omega m\)) or phase (in \(mrad\)) value for the corresponding cell.
\(log_{10}(\rho) (\Omega m)\) \(\phi (mrad)\)
.pha files¶
Structure is similar to the .mag files, except that the third columns contains the element phase values in mrad.
run.ctr¶
Provides an overview of the inversion process. Due to the adaption to screen output, this file look somewhat garbled when viewed in a text editor.
If the inversion finished sucessfully, the used CPU time will be saved to the
file (grep "\^CPU" run.ctr)
voltXX.dat¶
voltXX.dat contains the modelled resistances and phases for all measurement
configurations for iteration XX.
Line 1: number of measurement configurations
Line 2-End: Column 1: current injection electrode pair
(CRTomo format, as defined in config.dat)
Column 2: potential reading electrode pair
(CRTomo format, as defined in config.dat)
Column 3: resistance value in Ohm
Column 4: phase value in mrad
mod/¶
crt-files/volt.dat¶
volt.dat contains the modeled or measured resistances (not resistivities)
for all measurement configurations defined in config.dat. Multiple input
formats are currently recognized. The input formats are partially determined by
external switches and partially by certain key structures in the files
themselfs:
External switches:
DC or complex inversion/fpi (ldc)
Key structures:
individual errors (lindiv - determined from the first line of the file itself)
there are two basic file formats recognized, the “CRTomo standard” and the “industry standard”.
The format of volt.dat is explained by means of example files:
DC/Complex/FPI case, CRTomo standard:
3
10002 40003 4.3 -0.1
20003 50004 2.3 -0.2
30004 60005 9.2 -0.6
Line 1: number of measurement configurations (here: 3)
- Line 2-End:
Column 1: current injection electrode pair (CRTomo format, as defined in config.dat)
Column 2: potential reading electrode pair (CRTomo format, as defined in config.dat)
Column 3: resistance value in \(\Omega\) (CRTomo uses a current of 1 A, thus this value can also be interpreted as a voltage!)
Column 4: phase value (\(\varphi\)) in mrad
DC case individual errors:
3 T
10002 40003 4.3 0.43
20003 50004 2.3 0.23
30004 60005 9.2 0.92
1
Line 1 contains the number of measurements, plus the activation switch for the individual errors.
- Lines 2-(End-1):
Column 1: current injection electrode pair (CRTomo format, as defined in config.dat)
Column 2: potential reading electrode pair (CRTomo format, as defined in config.dat)
Column 3: resistance value in \(\Omega\) (CRTomo uses a current of 1 A, thus this value can also be interpreted as a voltage!)
Column 4: Normalized individual error (see last line)
Last line: Square root of the normalization factor of individual errors: \(\sqrt{\Delta R_{norm}}\)
Each individual error is computed using the value in column 4, multiplied with the inverse square of the normalization factor: \(\Delta R_i = R_i / \Delta R_{norm} ^ 2\). Also note that the input here is always linear, despite the inversion being formulated as log(R). Common values for the normalization factors, are as follows. To increasing error parameters by a factor of
2, use a norm factor of 0.7
3, use a norm factor of 0.577
0.5, use a norm factor of 1.4
0.33, use a norm factor of 1.73
Complex/FPI case:
3 T
10002 40003 4.3 -5 0.43 0.05
20003 50004 2.3 -10 0.23 0.1
30004 60005 9.2 -200 0.92 2
1 1
Line 1 contains the number of measurements, plus the activation switch for the individual errors.
- Lines 2-(End-1):
Column 1: current injection electrode pair (CRTomo format, as defined in config.dat)
Column 2: potential reading electrode pair (CRTomo format, as defined in config.dat)
Column 3: resistance value in \(\Omega\) (CRTomo uses a current of 1 A, thus this value can also be interpreted as a voltage!)
Column 4: phase values [mrad]
Column 5: Normalized individual magnitude error (see last line)
Column 6: Normalized individual phase error (see last line)
Last line: Square root of the normalization factors of individual errors: \(\sqrt{\Delta R_{norm}} \sqrt{\Delta \varphi_{norm}}\)
pot/pot.dat¶
Each pot.dat contains the modelled potential distribution for the
corresponding current injection configuration defined in config.dat (assuming a
unit current of 1 \(A\)), i.e., the (consecutive) number in the file name
corresponds to the line number (+1) in config.dat. The potential values of
the individual elements are listed as determined in elem.dat.
- Line 1-End:
Column 1: x coordinate in m
Column 2: z coordinate in m
Column 3: real part of complex potential, [V]
Column 4: imaginary part of complex potential, [V]
rho/¶
rho.dat¶
rho.dat contains the resistivity distribution, i.e. the resistivity values
of the individual elements determined in elem.dat. The format of rho.dat is
explained by means of an example file:
2296 2296 elements (of type 8)
100.000000 -5 resistivity and phase of 1st element (in m)
100.000000 -10 .
100.000000 -13.4 .
. .
. .
. .
99.999756 0 .
99.999893 0 .
99.999954 0 resistivity and phase of 2296th element (in m)
Line 1: number of elements (of type 8)
- Line 2-End:
Column 1: resistivity in Ohmm
Column 2: phase in mrad